
[This is the web version of a paper written by me, Bobby Ulich, Richard Godfrey, and Andrew Banks. The PDF version is available here.]
1 Introduction
Presently, there is no active search to find MH370’s debris field on the seabed of the Southern Indian Ocean (SIO). The last search was conducted by Ocean Infinity, who consulted with official and independent researchers, and subsequently scanned the seabed along the 7th arc as far north as S25° latitude. Since then, independent researchers have continued to analyze the available data to understand what areas of seabed are the most likely, and why previous search efforts have been unsuccessful. The objective is to define a manageable area for conducting a new search of the seabed.
In a previous post [1], we presented an overview of Bobby Ulich’s research [2], aimed at more precisely locating the point of impact (POI) using statistical criteria that requires that random variables (such as the reading errors of the satellite data) are not correlated, i.e., are truly random. A subsequent post [3] describes the work of Richard Godfrey et al. [4] to analytically evaluate a large number of candidate flight paths using these and other criteria. The results of that work suggest that the final hours of the flight were due south in the Indian Ocean along E93.7875° longitude, which matches a great circle between the waypoint BEDAX (about 100 NM west of Banda Aceh, Sumatra) and the South Pole. The POI was estimated to lie close to the 7th arc around S34.4° latitude.
Work continues to evaluate candidate paths using an accurate integrated model that includes satellite data, radar data, flight dynamics, automated navigation, meteorological conditions, fuel consumption, drift models, and aerial search results. That exhaustive work is nearing completion, and documentation of the methods and the results is ongoing. Like the previous work [4], the ongoing work suggests that the final trajectory of MH370 was most likely along a due south path along E93.7875° longitude.
In the interest of providing information in a timely manner, we have chosen to recommend a search area based on this most likely path. A comprehensive paper which expands upon the methods and results presented in previous work [2,4], and provides further justification for the selected path, will be available in the near future.
2 Last Estimated Position (LEP)
Using the results of the analysis presented above, the last estimated position (LEP) is based on a final trajectory of a constant longitude of E93.7875°, which is consistent with the aircraft traveling due south from waypoint BEDAX towards the South Pole. The LEP is based on a location exactly on the 7th arc, and the uncertainty associated with the LEP helps define the limits of the recommended search area.
When the SDU logs onto the Inmarsat network, the SDU begins the log-on sequence by first transmitting a log-on request, which is followed some seconds later by transmitting a log-on acknowledge. For MH370, those were the final two transmissions, transmitted at 00:19:29 (BTO = 23,000 μs) and 00:19:37 (BTO = 49,660 μs), respectively. From past work [6,7], we also know that the BTO values for the log-on request and log-on acknowledge are “anomalous” in that the raw values are outliers that require a correction. Fortunately, the required corrections are repeatable, and can be determined by analyzing prior flights.
Using the Inmarsat transaction logs for MH371 and MH370 [8], the BTO log-on statistics from March 7, 2014, 00:51:00, to March 8, 2014, 16:00:00, were analyzed to determine what offsets might be applied to log-on requests and log-on acknowledges. There were 29 cases in which there was an R-channel burst just after the initial (R600) log-on request and subsequent (R1200) log-on acknowledge. Of those 29 cases, the number of packets in the burst was 3 for 20 bursts, 2 for 6 bursts, and 1 for 3 bursts. The average of each burst was used as the reference for the log-in request and log-on acknowledge. In 4 of the 29 cases, the correction for the log-on request was near zero, i.e., the BTO values were not anomalous, so only 25 cases were included for log-on request statistics.
For the log-on requests, the mean offset from the R-channel burst is 4,578 μs with a standard deviation of 94 μs. The maximum offset was 4,800 μs (+222 μs from the mean) and the minimum was 4,380 μs (-198 μs from the mean).
For the log-on acknowledge, we considered a correction of the form (a + N × W), where a is a constant, N is an integer, and W represents the delay per slot. We found that the standard deviation of the correction error (using the average of the R1200 burst as the reference) to be minimized for W = 7812.0 μs. That’s very close to the 7812.5 μs value suggested by the 128 Hz internal clock of the SDU. By forcing W=7812.5 μs, the mean error to the correction is 23 μs, and the standard deviation is 30 μs. The observed standard deviation is very close to the 29 μs that DSTG recommends to use for “normal” R1200 values [7]. The consistency of the standard deviation of the corrected anomalous values with the standard deviation of the values not requiring a correction is reassuring. The total correction to the BTO for log-on acknowledges is therefore (23 + N × 7812.5) μs.
Using these log-on corrections produces corrected BTO values at 00:19 equal to:
00:19:29: 23000 – 4578 = 18422 μs
00:19:37: 49660 – 23 – 4 × 7812.5 = 18387 μs
We combine these values to determine the BE value of BTO by using the inverse of the variance as weighting, yielding a BE value of BTO = 18,390 μs (σ = 29 μs). Using this BE value of BTO with the longitude of E93.7875° and an assumed geometric altitude of 20,000 ft results in a position of S34.2342° E93.7875° at 00:19:29, which we assign as the LEP.
3 Terrain Near the LEP
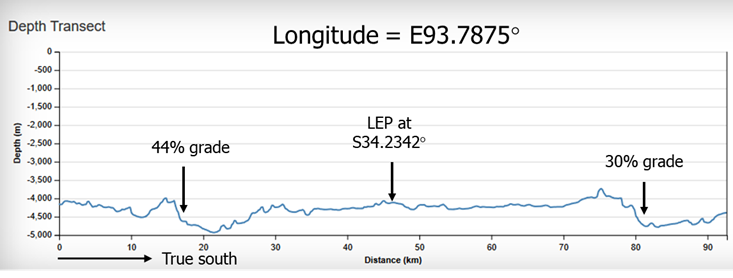
Figure 1 shows the subsea terrain in the vicinity of the LEP using data provided by Geosciences Australia [5]. Some of this area has already been searched by GO Phoenix (managed by the ATSB) using a towfish, and by Ocean Infinity (OI) using Seabed Constructor and its team of AUVs. However, as can be seen in Figure 1, some of the previously searched area has challenging terrain with steep slopes, and the debris field may have been either not detected due to terrain avoidance or shadows, or detected but not properly interpreted by reviewers. In particular, there is a steep slope that lies about 20 NM due south of the LEP that was not scanned by the towfish and appears to have been only partially scanned by the AUVs.

Figure 2 shows the ocean depth along a line of constant longitude in the vicinity of the LEP. The previously identified steep slope to the south of the LEP has a grade of about 30%. To the north, another slope has a grade of 44%. This slope was beyond the limits of the search boundaries of GO Phoenix, but was scanned by Seabed Constructor’s AUVs.
4 No Pilot Inputs after Fuel Exhaustion
In order to define the search area limits, we first consider no pilot inputs after fuel exhaustion. For this case, the search area limits are defined by the uncertainty of the LEP and the uncertainty of the uncontrolled flight path before impacting the ocean.
4.1 Uncertainty Due to BTO Noise
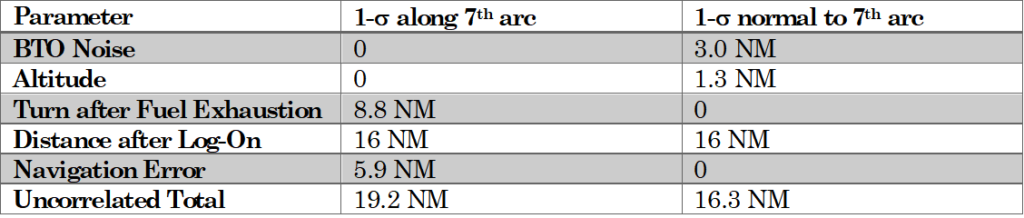
The uncertainty in the BTO produces a corresponding uncertainty in the position of the 7th arc. The calculated sensitivity of the arc position to the BTO is 0.104 NM/µs, i.e., a 1-µs increase in BTO pushes the 7th arc outward (southeast) by 0.104 NM. The 1-σ uncertainty of the arc position due to BTO noise is therefore 0.104 NM/µs × 29 µs = 3.0 NM.
4.2 Uncertainty Due to Altitude at 00:19:29
The LEP is based on an assumed altitude of 20,000 ft that is reached at 00:19:29, i.e., 1.5 to 2 minutes after fuel exhaustion. As the BTO represents the range between the aircraft and the satellite, the position of the 7th arc as projected on the surface of the earth depends on the altitude. As the aircraft would be between 0 and 40,000 ft at this time, we assign this altitude range as the 2-σ limits. The calculated sensitivity of the BTO to altitude is 12.8 µs/10,000 ft. The 1-σ uncertainty of the arc position due to altitude uncertainty is therefore 0.104 NM/µs × 12.8 µs = 1.33 NM.
4.3 Uncertainty of Turn Between Fuel Exhaustion and 00:19:29
Boeing conducted 10 simulations to determine the behavior of MH370 after fuel exhaustion with no pilot inputs [9] using a high-fidelity simulator for the 777-200ER aircraft. The trajectories for these simulations are shown in Figure 3. For each simulation, the autopilot was automatically disengaged after fuel exhaustion, and the aircraft turned slightly either to the right or to the left depending on a number of factors, including the electrical configuration, the initial conditions of the flight parameters, and the meteorological conditions. Within the 2-minute interval between fuel exhaustion and the log-on request at 00:19:29, the slight turn shifted the location that the aircraft crossed the 7th arc relative to where it would have crossed the 7th arc if the autopilot had remained engaged and the course was maintained. For the 10 cases, the lateral shift along the arc varied between 1.1 and 8.8 NM. As we don’t know how well the 10 cases represented the actual conditions, we conservatively assign a 1-σ uncertainty of 8.8 NM along the 7th arc due to the slight turn between fuel exhaustion and crossing the 7th arc.
4.4 Uncertainty of Trajectory Between 00:19:29 and the POI
In all 10 of the Boeing simulations, the aircraft banked after the autopilot was disengaged following fuel exhaustion. The magnitude and direction of the bank that develops is the net effect of a many factors, including thrust asymmetry, rudder inputs from the Thrust Asymmetry Compensation (TAC), rudder trim input, lateral weight imbalance, aerodynamic asymmetry, and turbulence, any of which increases the bank angle. On the other hand, the tendency to bank is opposed by the dihedral effect of the wings and the low center-of-mass. For all the simulations, the POI was within 32 NM from the 7th arc crossing at 00:19:29, as shown in Figure 3.
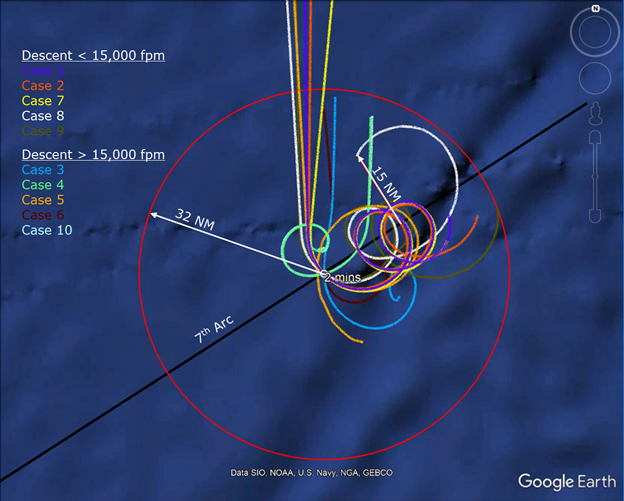
In some of those simulations, the bank was shallow, and phugoids lasting many minutes developed. In only 5 of the simulations did the rate of descent exceed 15,000 fpm while also experiencing a downward acceleration exceeding 0.67 g, which are the values of descent rate and downward acceleration derived from the two final values of the BFO. For these cases, the POI occurred between 4.7 and 7.9 NM from the point where the descent rate first exceeded 15,000 fpm. Other simulations of a banked descent after fuel exhaustion [10] suggest that an uncontrolled Boeing 777 would travel an additional distance of about 5 NM after a downward acceleration of 0.67 g and a rate of descent of 15,000 fpm simultaneously occur.
None of the Boeing simulations predict that the aircraft was in a steep descent as the 7th arc was crossed, so there is an unexplained discrepancy between the Boeing simulations and the descent rates derived from the final BFO values. In light of this discrepancy, we choose to not limit the distance traveled after crossing the 7th arc by only considering the distance traveled after the steep descent. Instead, we assign a 2-σ value of 32 NM for the distance traveled after crossing the 7th arc, based on the farthest distance that was observed in all 10 simulations, irrespective of the magnitude and timing of the descent rates.
4.5 Uncertainty Due to Navigation Error
There are two autopilot modes that could result in a trajectory that nominally follows a great circle between BEDAX and the South Pole. After passing BEDAX, if the autopilot remained in LNAV and the active waypoint was the South Pole (entered as 99SP, S90EXXXXX, or S90WXXXXX), the aircraft would fly along the longitude E93.7875° within the accuracy of the GPS-derived navigation. In this case, the expected navigational error would be much smaller than other sources of error, and can be safely ignored.
The other possibility is that after passing BEDAX, the autopilot was configured to fly along a constant true track (CTT) of 180°. Selecting this mode would require manually changing the heading reference switch from NORM to TRUE, as directions on maps, procedures, and in ATC communications are normally referenced to magnetic north, except in polar regions.
Unlike LNAV mode in which the cross-track error of the target path is continuously calculated and minimized, errors in track (which may be positive or negative) in CTT mode produce error in the due south path that may accumulate without correction. We assume here that that course is nominally 180° True, with a 1-σ uncertainty of 0.1 deg (0.001745 rad). As the distance between BEDAX and the 7th arc along the line of constant longitude is around 2365 NM, the cross-track error has a mean value of zero and a 1-s uncertainty of 4.1 NM. However, since the path crosses the 7th arc at an angle of 46 deg, the 1-σ uncertainty in position along the 7th arc is increased to 5.9 NM.
4.6 Search Area Based on No Pilot Inputs
Assuming there were no pilot inputs after 19:41, the uncertainties in the POI are summarized in Table 1. The 1-σ uncertainty along the 7th arc is 19.2 NM, and 16.3 NM normal to the 7th arc.
Table 1. Summary of POI Uncertainties Assuming No Pilot Inputs
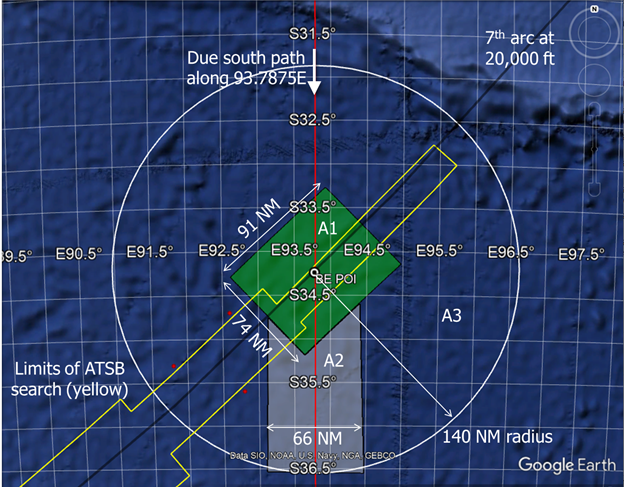
To achieve a confidence level of 98% requires searching an area defined by ±2.3-σ limits, with the LEP at its center. Based on this, the recommended area is 91 NM × 74 NM, and the total area is 6,719 NM2, or 23,050 km2. This area is depicted as A1 in Figure 4.
5 Controlled Glide Due South
We next consider the case in which there was a controlled glide after fuel exhaustion, which would extend the search area beyond the search area based on no pilot inputs. For a Boeing 777 gliding at an optimum speed, a glide ratio of about 20:1 can be achieved. This corresponds to a descent angle of 2.86°, and a continuous reduction in altitude of 1000 ft for every 3.29 NM traversed. Assuming an initial altitude of 42,400 ft (based on a standard altitude of 40,000 ft), the impact could be as far as 140 NM from the point of fuel exhaustion (ignoring the headwind at some altitudes, which would reduce the ground distance of the glide). If the glide started at a lower altitude, or if non-optimum airspeed was flown, the glide distance would be less. The uncertainty associated with the glide distance is much larger than other uncertainties, so we assume that with a glide, the POI might have been as far as 140 NM from the LEP, and use that as the southern limit.
The width of the search area as defined by a controlled glide is more difficult to estimate. If an experienced pilot wished to continue the flight path on a due-south course, that could be accomplished quite precisely. For example, if the autopilot mode was CTT before the fuel exhaustion, then a constant (true) track of 180 deg could be maintained using the indicated track shown in the navigation display. On the other hand, if the autopilot mode was LNAV before fuel exhaustion, then the cross-track error could be minimized by following the “magenta” line defined by the BEDAX-South Pole leg. In either case, the search area width could be limited to less than 10 NM to either side of the projected flight path.
Because we cannot be sure that there was an attempt to precisely follow a due south path, we assign a generous width to this part of the search area, centered on the due south path. A width of +/- 33 NM results in an additional search area of 6,300 NM2 (22,000 km2), and produces an area in similar size to A1. It is depicted as A2 in Figure 4.
6 Controlled Glide in an Arbitrary Direction
If there was a controlled glide that did not continue along the path flown prior to fuel exhaustion, it is nearly impossible to predict the direction. For instance, a path to the west would shield the pilot’s eyes from the rising sun to the east. A path to the northeast would extend the glide due to the tailwind. A path to the west would create more distance to the Australian shoreline. A path towards the northwest would be towards Mecca. Any of these directions is less likely than a continuation of the due south path, but it becomes nearly impossible to prioritize among these or other directions. Instead, we define area A3 as the circle with a radius of 140 NM, excluding the areas already included in A1 and A2. The area is roughly 48,400 NM2 (166,000 km2), and is depicted as A3 in Figure 4.
7 Conclusions
Recent analyses suggest that MH370’s flight path in its final hours followed E93.7875° longitude, corresponding to a great circle path between waypoint BEDAX and the South Pole. Using this result, the last estimated position (LEP) is S34.2342° E93.7875°. Although some of the subsea was previously searched in this vicinity, the terrain is challenging, and the debris field might have been not detected, or detected and misinterpreted. There is also the possibility that there was a controlled glide after fuel exhaustion, and an impact well beyond what was previously searched.
To define the search area near the LEP, three cases were considered, each with an associated search area. The highest priority search area of 6,719 NM2 (23,050 km2) assumes there were no pilot inputs after fuel exhaustion. The search area of next highest priority encompasses 6,300 NM2 (22,000 km2), and assumes there was a glide towards the south after fuel exhaustion. The lowest priority is the controlled glide in an arbitrary direction with an area of around 48,400 NM2 (166,000 km2).
8 References
[1] Iannello, “A New Methodology to Determine MH370’s Path”, May 31, 2019, https://mh370.radiantphysics.com/2019/05/31/a-new-methodology-to-determine-mh370s-path/
[2] Ulich, Technical Note presented in [1].
[3] Iannello, “A Comprehensive Survey of Possible MH370 Paths”, June 30, 2019, https://mh370.radiantphysics.com/2019/06/30/a-comprehensive-survey-of-possible-mh370-paths/, excerpted from [4].
[4] Godfrey, Ulich, Iannello, “Blowin’ In The Wind: Scanning the Southern Indian Ocean for MH370”, June 24, 2019, https://www.dropbox.com/s/9rpcnslz9g4izet/2019-06-30%20Blowing%20in%20the%20Wind%20-%20Scanning%20the%20Southern%20Indian%20Ocean%20for%20MH370.pdf
[5] “MH370 Data Release”, Geosciences Australia, https://www.ga.gov.au/about/projects/marine/mh370-data-release
[6] Ashton, Shuster-Bruce, College, Dickinson, “The Search for MH370”, The Journal of Navigation, Vol 68 (1), January 2015.
[7] Davey, Gordon, Holland, Rutten, Williams, “Bayesian Methods in the Search for MH370”, Defense, Science, and Technology Group, Australia, November 30, 2015.
[8] Iannello, “The Unredacted Satellite Data for MH370”, June 12, 2017, https://mh370.radiantphysics.com/2017/06/12/the-unredacted-inmarsat-satellite-data-for-mh370/
[9] Iannello, “End-of-Flight Simulations of MH370”, August 2018, https://mh370.radiantphysics.com/2018/08/19/end-of-flight-simulations-of-mh370/
[10] Iannello, “MH370 End-of-Flight with Banked Descent and No Pilot”, June 4, 2017, https://mh370.radiantphysics.com/2017/06/04/mh370-end-of-flight-with-banked-descent-and-no-pilot/
Update on March 12, 2020
The best estimate of the point of impact (BE POI) has been renamed the last estimated position (LEP), which is a more accurate description. The location is unchanged.